Template Matching in MATLAB

 The comparison of two images is done based on correlation coefficient. The quantitative measure of the degree of association of two distinct variables is often coined as correlation coefficient, which typically ranges between -1 and 1.

Pearson Correlation coefficient,  

Let’s start with the basics.

Steps to be performed for finding the correlation coefficient between two vectors or matrices.

This denotes that the matrix A and B are highly correlated.

MATLAB CODE:

Example: 1

A= [1 4 7; 2 5 8; 3 6 9]

B = A*2

%Find the average of the matrix A

meanA = mean2(A);

%Find the average of the matrix B

meanB = mean2(B);

%Subtract the average value from matrix A

Asub = A-meanA;

%Subtract the average value from matrix B

Bsub = B-meanB;

%Covariance of matrix A and matrix B

covAB = mean2(Asub.*Bsub);

%Find the standard deviation of the matrix A

stdA = std(A(:),1);

%Find the standard deviation of the matrix B

stdB = std(B(:),1);

%Find the correlation Cofficient

Rho = covAB./(stdA*stdB)

Example: 2

%Assign new values to B

B = [9 6 3;8 5 2; 7 4 1];

Rho = corr2(A,B)

EXPLANATION:

In the first example, both A and B are highly correlated. The correlation coefficient is 1, whereas in example 2, the correlation coefficient is -1.

                  Consider the reference image as template image which will be larger in size and search image as target image usually smaller in size.

In Principles of Digital Image processing, algorithm 11.1(pg.262), a clear explanation of template matching algorithm is given. 

Template Matching using MATLAB command ‘normcorrx2’:

MATLAB CODE:

%Read an Image A(Template)

A1 = imread('benten.jpg');

%Read the Target Image

B1 = imread('watch.jpg');

A = A1(:,:,1);

B = B1(:,:,1);

normx_corrmap=normxcorr2(B(:,:,1),A(:,:,1));

maxptx = max(normx_corrmap(:));

[x1,y1]=find(normx_corrmap==maxptx);

figure,

imagesc(A1(x1-size(B,1):x1,y1-size(B,2):y1,:));axis image

NOTE: ‘normxcorr2’ is the normalized cross correlation.

Template Matching in Spatial Domain:

MATLAB CODE:

%Read an Image A(Template)

A1 = imread('benten.jpg');

%Read the Target Image

B1 = imread('watch.jpg');

A = A1(:,:,1);

B = B1(:,:,1);

corr_map = zeros([size(A,1),size(A,2)]);

for i = 1:size(A,1)-size(B,1)

    for j = 1:size(A,2)-size(B,2)

        %Construct the correlation map

        corr_map(i,j) = corr2(A(i:i+size(B,1)-1,j:j+size(B,2)-1),B);

    end

end

figure,images(corr_map);colorbar;

%Find the maximum value

maxpt = max(corr_map(:));

[x,y]=find(corr_map==maxpt);

%Display the image from the template

figure,imagesc(B1);title('Target Image');colormap(gray);axis image

grayA = rgb2gray(A1);

Res   = A;

Res(:,:,1)=grayA;

Res(:,:,2)=grayA;

Res(:,:,3)=grayA;

Res(x:x+size(B,1)-1,y:y+size(B,2)-1,:)=A1(x:x+size(B,1)-1,y:y+size(B,2)-1,:);

figure,imagesc(Res);

EXPLANATION:

MATLAB command ‘corr2’ is used to find the correlation coefficient. The Target Image is placed over the template image and correlation coefficient for each pixel in the template image is found to construct the correlation map. After sliding through all the pixels in the template image, the maximum coefficient is obtained from the map. The pixel position with maximum value is the starting point of the target image.

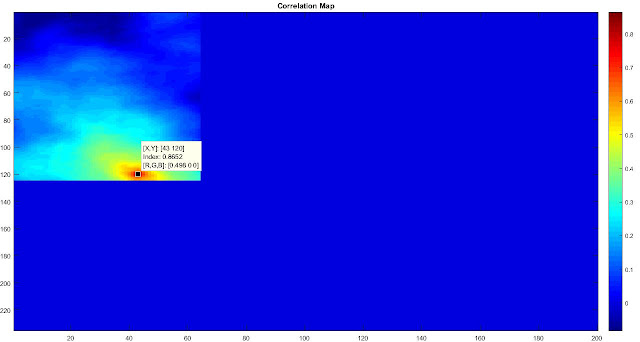
In the above example, maximum value is 0.8652 and the pixel positions corresponding to this value in correlation map(x,y) is (120,43)

Template Image


+   

Target Image


=

Template Matching in Frequency or Fourier Domain:

%Read two images of same scene

A = imread('Image1.jpg');

B = imread('Image2.jpg');

figure,subplot(2,1,1);imagesc(A);title('Image 1');axis image

subplot(2,1,2);imagesc(B);title('Image 2');axis image

%Crop a part from the image matrix B

B = imcrop(B,[58.5 49.5 226 102]);

figure,imagesc(B);title('sub Image - Image 2');axis image

%Pad the image matrix B with zeros

B1 = zeros([size(A,1),size(A,2)]);

B1(1:size(B,1),1:size(B,2))=B(:,:,1);

%Apply Fourier Transform

Signal1 = fftshift(fft2(A(:,:,1)));

Signal2 = fftshift(fft2(B1));

%Mulitply Signal1 with the conjugate of Signal2

R = Signal1 .*conj(Signal2);

%Normalize the result

Ph = R./abs(R);

%Apply inverse fourier transform

IFT = ifft2(fftshift(Ph));

figure,imagesc((abs((IFT))));colormap(gray);

Correlation Map

%Find the maximum value

maxpt = max(real(IFT(:)));

%Find the pixel position of the maximum value

[x,y]= find(real(IFT)==maxpt);

figure,subplot(1,2,1);imagesc(A(x:x+size(B,1),y:y+size(B,2),:));axis image

subplot(1,2,2);imagesc(B);axis image

EXPLANATION:

The above implementation is based on normalized cross correlation in Fourier domain.Also known as phase correlation. The two images used here are different snapshots of the same scene.  ‘Image1.jpg’ is used as template image and a sub image from the ‘Image2.jpg’ is used as target image. The target image is padded with zeros to match the size of the template image. After Fourier transform, the template signal is multiplied with the conjugate of the target signal and normalized. Then inverse Fourier is applied and the pixel position corresponding to the maximum value is extracted.

The maximum value is 0.0374 and the pixel positions (x,y) is(59,78). From the correlation map, it is evident that the maximum value is at the pixel position(59,78).